【Python】割線法-方程式の数値解とグラフ出力、黄金比収束

割線法（セカント法）は、非線形方程式の数値解法の一つで、
関数の解を近似的な接線（割線）を用いて求める手法です。

主に、ニュートン法が使えない関数の解を求めるときに使用します。

【Python】ニュートン法-例題で方程式の解とグラフを出力

Pythonでニュートン法（ニュートンラプソン法）による解の導出をします。公式の紹介や原理等に触れていつ使うかなど含めて解説しています。

alicia-ing.com

2024.10.24

本記事では、ニュートン法と比較しながらPythonを使って二分法を表現します。

割線法とニュートン法の違い

非線形方程式や連立方程式など解析的に解けない方程式は、
ニュートン法のような反復法を用いて、解を求めます。

しかし、ニュートン法は示した漸化式から分かるように、
導関数\(f^{\prime}(x)\)がなければ使えないアルゴリズムです。

$$x_{2}=x_1-\frac{f(x_1)}{f^{\prime}(x_1)}$$

導関数\(f^{\prime}(x)\)が使えないことは、関数\(f(x)\)の接線がないことを意味しています。

そこで、接線の代わりに関数\(f(x_0)\)と\(f(x_1)\)を通る直線を用いて、
\(x\)軸上の\(x_2\)を求める手法が割線法です。

$$f^{\prime}(x_1)\simeq\frac{f(x_1)-f(x_0)}{x_1-x_0}$$

導関数\(f^{\prime}(x_1)\)は接線の式から得た近似式で、
この式をニュートン法の式に代入すると、\(x\)軸上の\(x_2\)は、

$$x_{2}=x_1-\frac{f(x_1)(x_1-x_0)}{f(x_1)-f(x_0)}$$

となります。得た式を一般化すると、次の漸化式になります。

$$x_{n+2}=x_{n+1}-\frac{f(x_{n+1})(x_{n+1}-x_{n})}{f(x_{n+1})-f(x_{n})}$$

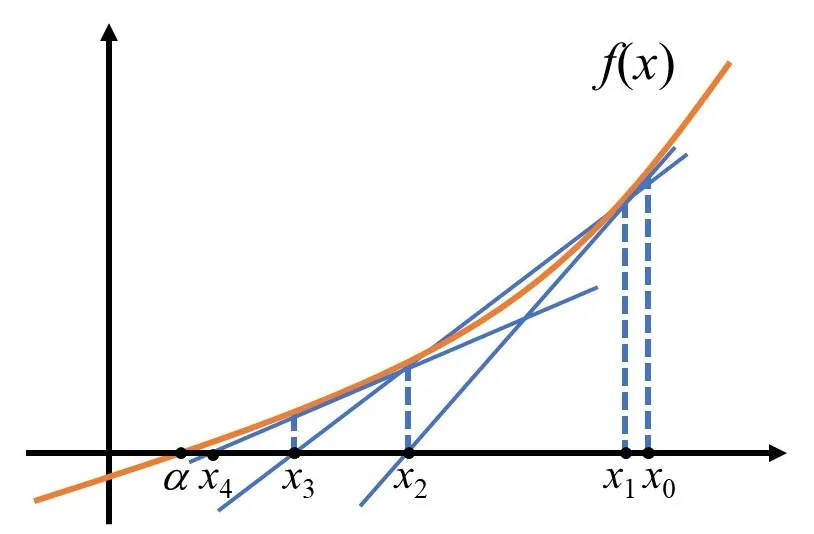
以上までが割線法の基本的なアルゴリズムになります。

ニュートン法のように関数\(f(x)\)の導関数を求める必要がないため、計算コストが低いです。

また、初期の推定解を選ぶ柔軟性があります。
これにより、導関数の計算が難しい場合やコストを抑えたい場合に有用です。

Pythonで表現

Pythonで割線法を使用して解を表現します。

読者の方であれば、解は\(x＝\pm\sqrt{ 2 } \)だと分かるかと思いますが、
この値を割線法で考えます。

【Python】 統計処理・データ分析で必要なライブラリ一覧

Pythonの統計処理で使うライブラリ「Numpy・Matplotlib・Pandas・Scipy」を紹介。さらにGoogle Colaboratoryでの処理も解説。

alicia-ing.com

2024.10.27

ソースコード

def f(x):
    return x**2 - 2

def secant_method(default, precision=1e-8, max_step=100):
    x0 = default
    x1 = default + 0.01  # 少し離れた点を選ぶことで近似的に接線とみなせる。
    step = 0

    while abs(f(x1)) > precision:
        print(f"反復 {step}: x{step} = {x0}, x{step+1} = {x1}, f(x{step}) = {f(x0)}, f(x{step+1}) = {f(x1)}")
        x_temp = x1 - f(x1) * (x1 - x0) / (f(x1) - f(x0))
        x0 = x1
        x1 = x_temp
        step += 1

        if step >= max_step:
            raise RuntimeError("収束しませんでした。")

    print(f"\n方程式の解: {x1}")
    return x1

# 初期値
default = 1.0

# 割線法を実行
result = secant_method(default)

UdemyでPythonを学習

Udemyは、オンデマンド式の学習講座です。
趣味から実務まで使えるおすすめの講座を紹介します。

ビックセール開催中（11月29日まで）
対象のコースが1300円から（最大95%OFF）

最大95%OFF

終了まで

時間

：

分

：

秒

解説

\(f(x)\)は関数\(f(x)=x^2-2\)を定義します。

secant_method関数は、与えられた初期値defaultを\(x_0\)に代入し、
さらにもう1点\(x_1\)は\(x_0\)に近い地点で開始します。

２点が近いことで接線を近似することが可能です。

指定された収束条件 (精度)precisionと最大反復回数max_stepを使用して、割線法を実行します。

whileループ内で、反復ごとに\(x\)、\( f(x)\)を表示します。
反復0であれば、\(x_0\)、\(x_1\)、\( f(x_0)\)、\( f(x_1)\)を出力して、
次のステップに更新します。

\(|f(x_1)|\gt\)precision が収束条件であり、
指定された精度に達するまで反復が続きます。

もし最大反復回数に達した場合はRuntimeErrorが発生し、
収束しなかった旨が表示されます。

反復の回数が収束条件を満たすと、方程式の解が得られます。

実行例

Google Colaboratoryで実行しています。

初めを０として、収束条件であり、指定された精度に達するまで反復します。
最終的に、収束条件を満たす方程式\(f(x) =0\)の解を出力します。

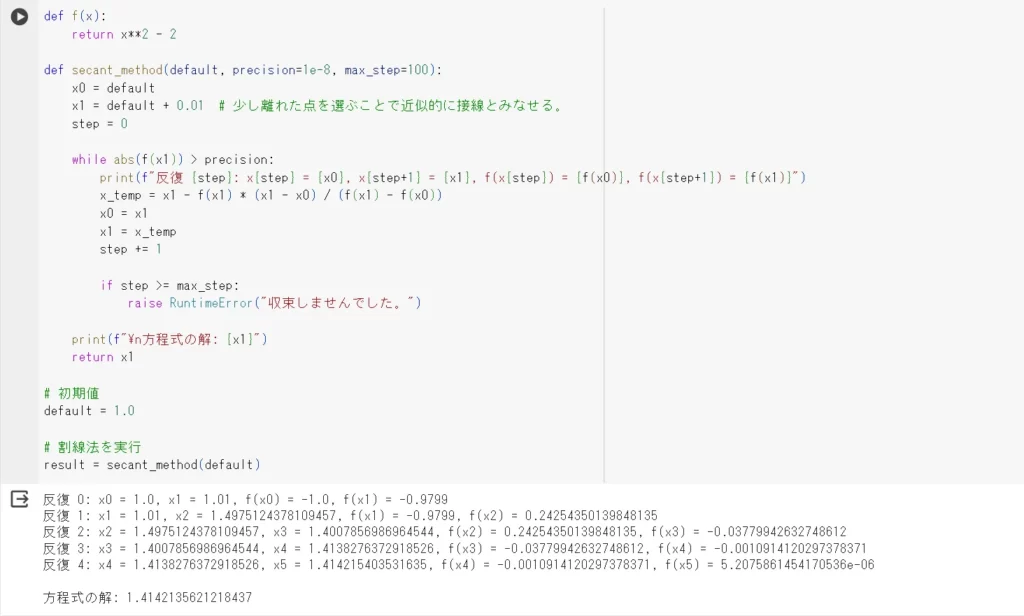
方程式の解\(\alpha\)は、\(\alpha\simeq1.414213\)でこの数値は、\(\sqrt{2}\)の数値解です。

グラフの描画

方程式の解の妥当性をグラフで確認します。

解は、\(f(x) =0\)となる\(x \)軸上の\(x \)の値になります。

先ほどのソースコードに続けてグラフと解をプロットします。

# グラフのプロット
plt.figure(figsize=(10, 6))
plt.axhline(0, color='black',linewidth=0.5)
plt.axvline(0, color='black',linewidth=0.5)
x_vals = np.linspace(min(x_values_secant) - 1, max(x_values_secant), 100)
plt.plot(x_vals, f(x_vals), label='f(x)')
plt.scatter(x_values_secant, f_values_secant, color='red', label='Secant Method Iterations')
plt.scatter(result_secant, f(result_secant), color='purple', marker='x', label='Secant Method Solution')
plt.xlabel('x')
plt.ylabel('f(x)')
plt.title('Secant Method')
plt.legend()
plt.show()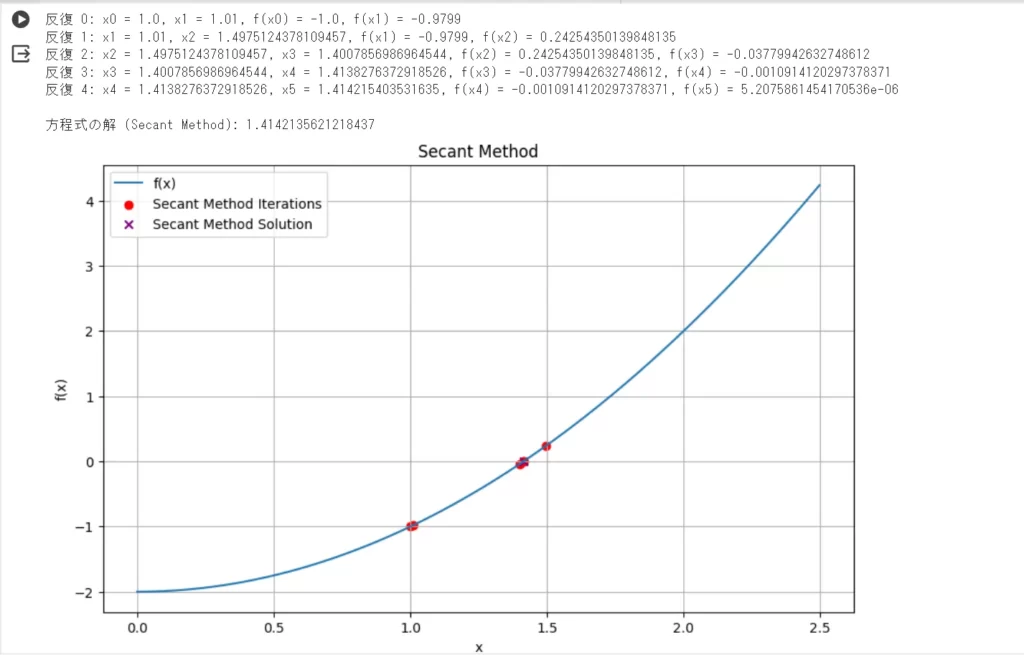

\(f(x) =0\)の\(x\)軸上に方程式の解がプロットされています。

収束の速さの比較

方程式\(f(x)＝x^2-2=0 \)を用いて、ニュートン法と割線法の収束性を比較します。

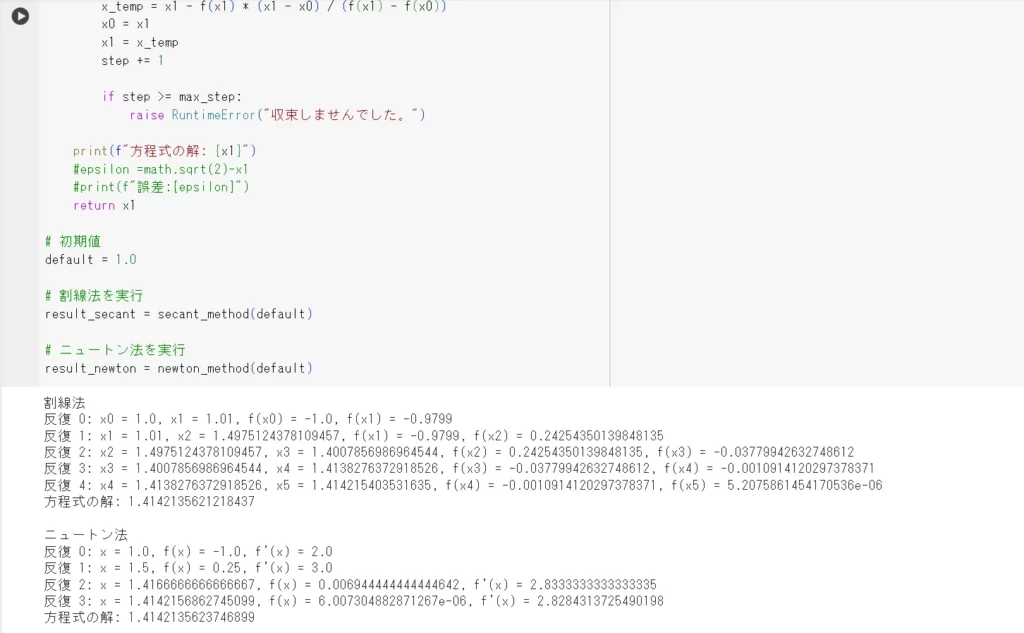
割線法は反復回数4に対して、ニュートン法は反復回数3です。
このことから、割線法の方が収束が遅いことを示しています。

【Python】２分法で方程式の解とグラフを出力ー収束性の比較

２分法は、非線形方程式の数値解を求めるための反復的な数値計算手法の一つで、連続関数において、閉区間に方程式の解を一つ持たせて、中間値の定理で、解を表現します。ニュートン法や割線法に比べて収束は遅いですが、発散することなく安定しています。

alicia-ing.com

2024.11.10

黄金比

割線法について、数列\({x_n}\)が解\(x＝\alpha \)に\(p\)次収束することを考えます。
\(p\)の2次方程式\(p^2＝p+1\)が得られて、正の解は、

$$p=\frac{1+\sqrt{5}}{2}\simeq1.618$$

となります。一般に割線法は方程式の解によらず、1.618次収束をします。この値を用いた\(1:1.618\)は黄金比と呼ばれ、デザインを美しくする比率として使用されます。

例えば、名刺やクレジットカードなどのカード類、ピラミッド、パルテノン宮殿のような建造物やモナ・リザのような肖像画に使用されています。

ライブラリで割線法を表現

scipy.optimizeモジュールを使うと、割線法を用いた方程式の解の近似ができます。

from scipy.optimize import fsolve

def f(x):
    return x**2 - 2

# 初期値
default = 1.0

# 割線法（セカント法）の実行・表示
result_secant = fsolve(f, default)
print(f"方程式の解: {result_secant}")

まとめ

割線法（セカント法）は、非線形方程式の数値解を求めるための反復的な数値計算手法の一つです。

ニュートン法と同様に、初期推定値から方程式の解に収束するように逐次的な近似を行います。
一方でニュートン法とは異なり、導関数（接線の傾き）を用いる代わりに、近似的な接線を前回の推定点と現在の推定点を通る直線として用います。

導関数を計算する必要がないので、導関数を計算できない場合にも適用できます。ただし、収束の速さはニュートン法よりも遅いので、計算量は増えます。