2分法は、数学的な方程式や関数の根を見つける手法の一つです。この方法は、区間を狭めていくことで、解に近づいていきます。
2分法はニュートン法や割線法(セカント法)などのように、解の候補となる数列\(x_0\),\(x_1\)…を発生させるのではなく、解の存在区間を縮小させていく考え方(区間縮小法)です。
本記事では、2分法のアルゴリズムをPythonを使って表現します。
2分法の基本原理
方程式の解は、グラフでは\(x\)軸上に存在します。
ある実数\(a\)と\(b\)について\(f(a)f(b)\leq0\)であれば、\(f(a)\)と\(f(b)\)は異符号になります。(いずれかが0である厳密性はここでは考慮しません。)
このとき、関数\(f(x)\)が連続関数であれば、方程式の解を\(\alpha\)として、\(f(\alpha)=0\)は閉区間\([a,b]\)内に少なくとも1つ存在します。(中間値の定理)
区間の中点\(c=\frac{a+b}{2}\)において、\(f(a)f(c)\leq0\)であれば\(c\)を\(b\)とみなして、方程式の解\(f(\alpha)=0\)は閉区間\([a,c]\)内に縮小できます。
一方で、\(f(a)f(c)\leq0\)であれば\(c\)を\(a\)とみなして、閉区間\([c,b]\)内に縮小できます。
この処理を反復して、閉区間内に必ず解を含みながら、区間の幅を\(\frac{1}{2}\)ずつ縮小する手法が2分法です。
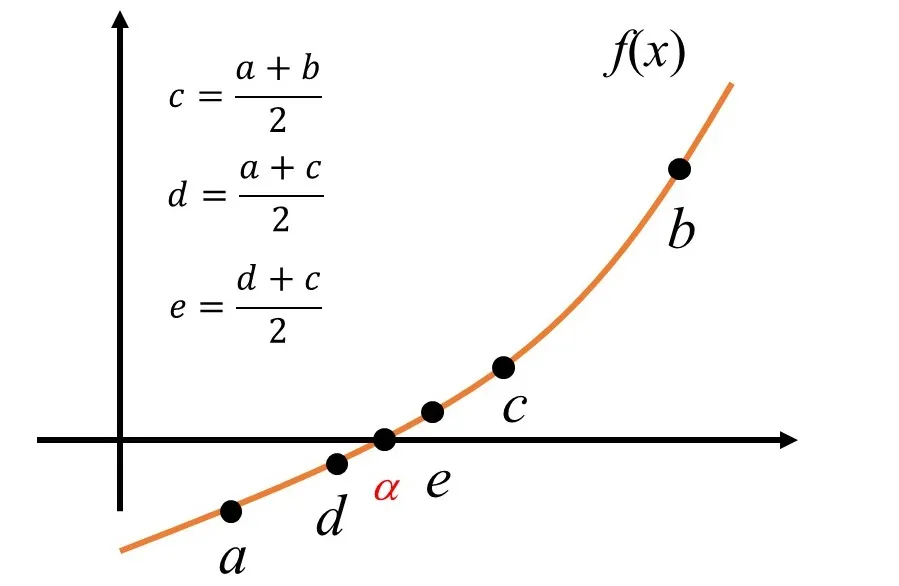
- \(a\)と\(b\)を区間の初期値として設定。(\(a\lt b\),\(f(a)f(b)\leq0\)を満たす)
- 区間の中点\(c\)を設定。
- 関数\(f(c)\)の値を計算し、その符号を確認。解が存在する方向の区間\([a,c]\)または\([c,b]\)に絞り込む。
この操作を繰り返して、方程式の解\(\alpha\)の値に近似させます。
Pythonで2分法を表現
Pythonで2分法を使用して解を表現します。
\(f(x)=x^2-2=0 \)を2分法で解く。
方程式\(f(x)\)の解は、\(x=\pm\sqrt{ 2 }\simeq1.414\)なので、この値の間で初期値を設けます。
ソースコード
def f(x):
return x**2 - 2
def bisection_method(a, b, precision=1e-8, max_step=100):
step = 0
while (b - a) / 2 > precision:
c = (a + b) / 2
print(f"反復 {step}: a{step} = {a}, b{step} = {b}, c{step} = {c}, f(a{step}) = {f(a)}, f(b{step}) = {f(b)}, f(c{step}) = {f(c)}")
if f(c) == 0:
print(f"\n方程式の解: {c}")
return c
elif f(c) * f(a) < 0:
b = c
else:
a = c
step += 1
if step >= max_step:
raise RuntimeError("収束しませんでした。")
print(f"\n方程式の解: {(a + b) / 2}")
return (a + b) / 2
# 初期値
a = 1.0
b = 2.0
# 2分法を実行
result = bisection_method(a, b)UdemyでPythonを学習
Udemyは、オンデマンド式の学習講座です。
趣味から実務まで使えるおすすめの講座を紹介します。
- 現役シリコンバレーエンジニアが教えるPython 3 入門 + 応用 +アメリカのシリコンバレー流コードスタイル
Pythonをインストールから環境設定、基本文法が学習
さらに暗号化、インフラ自動化、非同期処理についても学べます。
Pythonを基礎から応用まで学びたい人におすすめ
- みんなのAI講座 ゼロからPythonで学ぶ人工知能と機械学習 【2024年最新版】
機械学習ライブラリで文字認識や株価分析などを行う。
人口知能やニューラルネットワーク、機械学習を学びたい人におすすめ。
- 【世界で55万人が受講】データサイエンティストを目指すあなたへ〜データサイエンス25時間ブートキャンプ〜
統計分析、機械学習の実装、ディープラーニングの実装を学習。
データサイエンティストになりたい人におすすめ。
- 0から始めるTkinterの使い方完全マスター講座〜Python×GUIの基礎・応用〜
TkinterのGUIを作成から発展的な操作までアプリ実例を示して学習。
アプリ開発したい人におすすめ。
解説
\(f(x)\)は、与えられた方程式\(f(x)=x^2-2\)を表す関数です。
bisection_method関数は、2分法を用いて方程式の解を求める関数です。
引数として初期の区間 \([a, b]\)、収束の精度 precisionと最大反復回数max_stepを取ります。
whileループでは、解の存在する範囲\([a, b]\)の中点\(c\)を計算しています。
各反復で、\(c\)の関数値\(f(c)\)を評価し、解が見つかればその値を出力して終了します。
\(f(a)f(c)\leq0\) であれば、解は\([a, c]\)の範囲にあり、それ以外の場合は解は\([c, b]\)に範囲を狭めます。
初期値a、bは1.0、2.0としています。
この値は、方程式\(f(x)=x^2-2\)の解の間である必要があるので、(a=5.0、b=10.0)のように選択していけません。
実行例
Google Colaboratoryで実行しています。
初めを0として、収束条件であり、指定された精度に達するまで反復します。
最終的に、収束条件を満たす方程式\(f(x) =0\)の解を出力します。
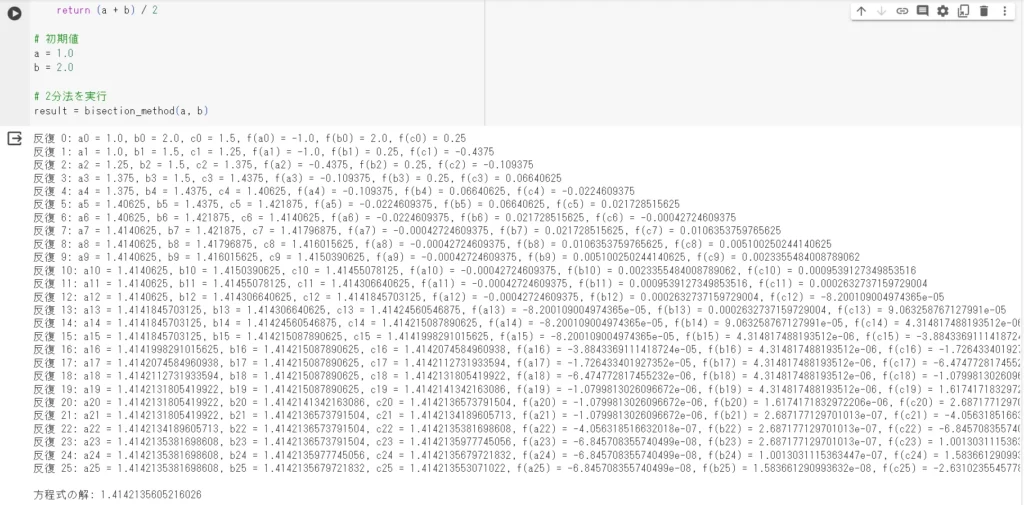
グラフ描画
得た方程式の解の妥当性を先ほどのソースコードに続けてグラフと解をプロットします。
解は、\(f(x) =0\)となる\(x \)軸上の\(x\)の値になります。
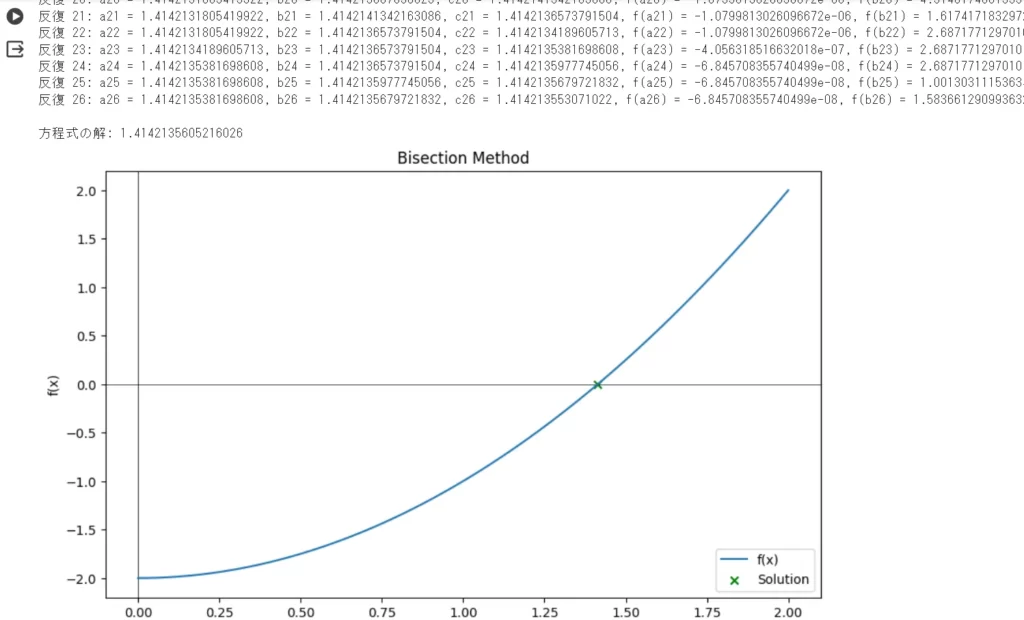
方程式の解は、(x)軸上に方程式の解がプロットされています。
収束の速さ
2分法は、区間の幅を\(\frac{1}{2}\)ずつ縮小する1次収束なので、ニュートン法と割線法と比較して、収束は遅いです。
一方で、ニュートン法や割線法は発散してしまう可能性がありますが、2分法は収束性が高いです。
ライブラリで2分法を表現
scipy.optimizeモジュールを使うことで、2分法で方程式の解の近似ができます。
from scipy.optimize import bisect
def f(x):
return x**2 - 2
# 初期値
a = 0.0
b = 2.0
# 2分法を実行
result_bisection = bisect(f, a, b)
# 結果の表示
print(f"方程式の解: {result_bisection}")
まとめ
2分法は、非線形方程式の数値解を求めるための反復的な数値計算手法の一つです。
連続関数において、ある実数\(a\)と\(b\)について\(f(a)f(b)\leq0\)であれば、閉区間\([a,b]\)に方程式の解を一つ持ちます。
このアプローチは、中間値の定理に基づいており、初期値が解の前後にあることを前提としています。
ニュートン法や割線法に比べて収束は遅いですが、2分法は収束性は高いので発散することなく、比較的安定しています。






