ニュートン法(またはニュートン・ラフソン法)は、関数の根(方程式がゼロとなる点)、最小値、最大値などを求めるための反復的な数値解法です。
数学やコンピューターサイエンスの分野では、方程式の解を求めたり、最適化問題に取り組んだりする際に様々な手法があります。
本記事では、これらを求めるアルゴリズムの一つニュートン法をPythonを使って表現します。
ニュートン法の基本原理
与えられた関数\(f(x) \)の方程式がゼロになる点を求めるためには、以下のステップで構成されます。
- \(x_0 \)を初期値の推定値として設定。
- \(f(x_0) \)を求めて、\(x_0 \)の接線の式から\(y=0 \)と交わる\(x\)軸上の点\(x_1 \)を設定。
- 同様に、\(f(x_1) \)を求めて、接線の式から\(x_2 \)を設定。
この操作を繰り返して、\(f(x)=0 \)となる\(x=\alpha \)の値に近似させます。
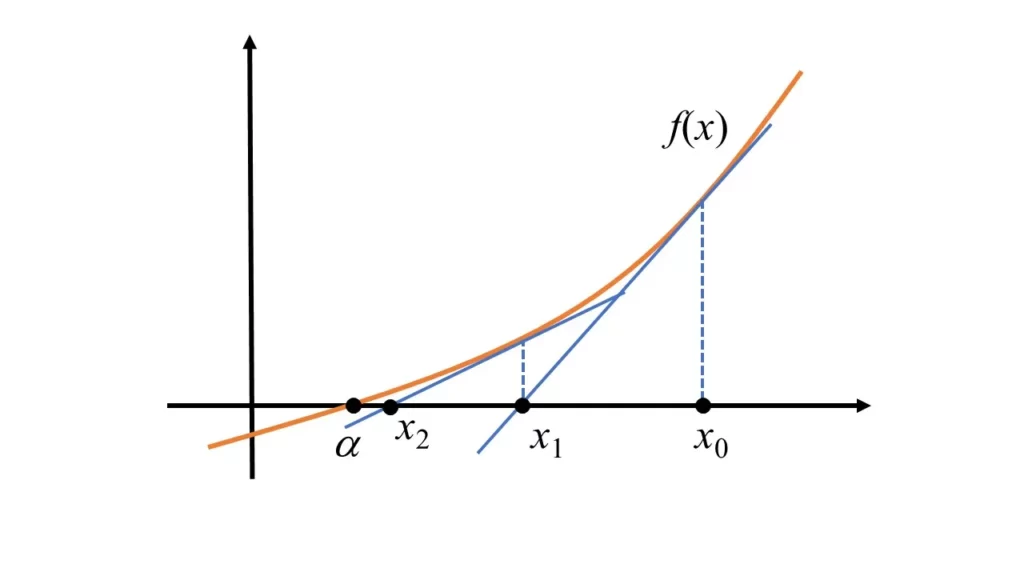
一連の操作は、接線の式を変形して、ニュートン法の公式として一般化されます。
$$f(x_n)=f^{\prime}(x_n)(x_n-x_{n+1}) \Longleftrightarrow x_{n+1}=x_n-\frac{f(x_n)}{f^{\prime}(x_n)} $$
\(f(x_n)=f^{\prime}(x_n)(x_n-x_{n+1}) \) \(\Longleftrightarrow x_{n+1}=x_n-\frac{f(x_n)}{f^{\prime}(x_n)}\)
ニュートン法の式から分かるように、導関数\(f^{\prime}(x)\)がない場合には、使用することができません。
そのような関数の場合は、関数\(f(x)\)上に初期値を2点設けて、近似的に接線とみなして方程式の解を求める方法があります。
この手法を割線法(セカント法)といいます。
ニュートン法が有用な状況
ニュートン法は、利点もありますが、同時に使用する上で注意点があります。
- 収束速度
初期値が解に近い場合、収束が非常に速い。 - 広範な適用
非線形方程式や最適化問題、回帰分析、機械学習など、さまざまな分野で使用可能。
- 初期値の選定
収束が初期値に依存するため、良い初期値の選定が重要。 - 発散の可能性
特定の条件下で発散する可能性があるため、注意が必要。
ニュートン法が適用できる場面は多岐に渡っています。
- 方程式や根の求解
非線形方程式や関数の根を求めることに非常に有効で、特に初期値が解に近い場合、収束が非常に速い傾向があります。 - 最適化問題
最小値や最大値を見つけるための最適化問題にも使用されます。関数の極小点や極大点を求めたい場合、その点での導関数がゼロになるため、ニュートン法が適用できます。 - 数値解析
微分可能な関数に対して適用できて、高い収束速度が特徴なので、数値解析の分野で幅広く使用されます。 - 回帰分析
パラメータの最適化や尤度関数の最大化などに応用できるので、回帰分析に使用されます。 - 機械学習
ニュートン法を拡張した準ニュートン法が機械学習の最適化問題に適用されます。
Pythonで表現
Pythonでニュートン法を使用して解を表現します。
\(f(x)=x^2-2=0 \)をニュートン法で解く。
読者の方であれば、解は\(x=\pm\sqrt{ 2 } \)だと分かるでしょうが、この値をニュートン法で考えます。
ソースコード
def f(x):
return x**2 - 2
def df(x):
return 2*x
def newton_method(default , precision=1e-8, max_step=100):
x = default
step = 0
while abs(f(x)) > precision:
print(f"反復 {step}: x = {x}, f(x) = {f(x)}, f'(x) = {df(x)}")
x = x - f(x) / df(x)
step += 1
if step >= max_step:
raise RuntimeError("収束しませんでした。")
print(f"\n方程式の解: {x}")
return x
# 初期値
default = 1.0
# ニュートン法を実行
result = newton_method(default)UdemyでPythonを学習
Udemyは、オンデマンド式の学習講座です。
趣味から実務まで使えるおすすめの講座を紹介します。
- 現役シリコンバレーエンジニアが教えるPython 3 入門 + 応用 +アメリカのシリコンバレー流コードスタイル
Pythonをインストールから環境設定、基本文法が学習
さらに暗号化、インフラ自動化、非同期処理についても学べます。
Pythonを基礎から応用まで学びたい人におすすめ
- みんなのAI講座 ゼロからPythonで学ぶ人工知能と機械学習 【2024年最新版】
機械学習ライブラリで文字認識や株価分析などを行う。
人口知能やニューラルネットワーク、機械学習を学びたい人におすすめ。
- 【世界で55万人が受講】データサイエンティストを目指すあなたへ〜データサイエンス25時間ブートキャンプ〜
統計分析、機械学習の実装、ディープラーニングの実装を学習。
データサイエンティストになりたい人におすすめ。
- 0から始めるTkinterの使い方完全マスター講座〜Python×GUIの基礎・応用〜
TkinterのGUIを作成から発展的な操作までアプリ実例を示して学習。
アプリ開発したい人におすすめ。
解説
f(x)とdf(x)ではそれぞれ関数\(f(x)=x^2-2\)とその関数を微分した導関数\(f^{\prime}(x)=2x\)を定義します。
関数は、初期値 default を受け取り、指定された収束条件 (精度)precision と最大反復回数 max_step を使用して、ニュートン法を実行します。
while ループ内で、反復ごとに現在の\(x\)、\( f(x)\)、\(f^{\prime}(x)\)を表示し、次のステップに更新します。
反復が指定された収束条件を満たす。あるいは最大反復回数に達すると、最終的に方程式の解が得られます。
理想は関数\(f(x) =0\)となるときの解を得たいです。
しかし、精度に0を代入すると反復数を超えて収束しないので、限りなく0に近い値を用意します。
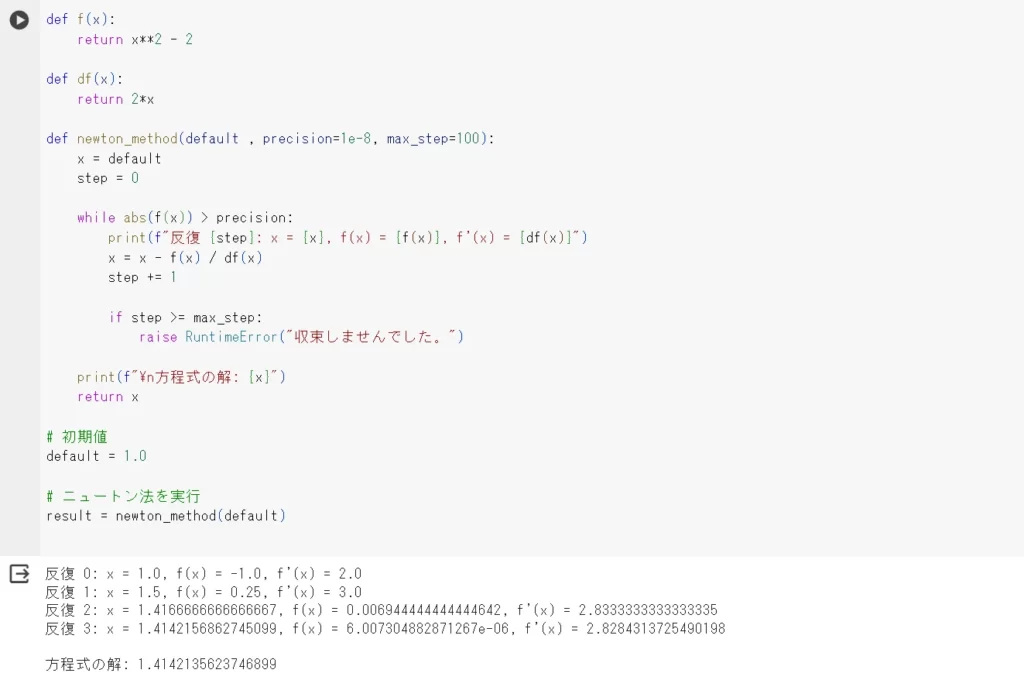
実行例
実行環境は、Google Colaboratoryを使用します。
初めを0として、精度が低ければ反復回数を増やします。
最終的に、関数\(f(x) =0\)となる方程式の解を出力します。
グラフ描画
次に、方程式の解が正しいかグラフを用いて確認します。
解は、\(f(x) =0\)。要するに、\(x \)軸上の\(x \)の値になります。
先ほどのソースコードに続けてグラフと解をプロットします。
# 関数のグラフと解の位置をプロット
x_vals = np.linspace(0, default, 100)
plt.plot(x_vals, f(x_vals), label="f(x)")
plt.scatter(result, f(result), color='red', label="Solution")
# グラフの装飾
plt.axhline(0, color='black',linewidth=0.5)
plt.axvline(0, color='black',linewidth=0.5)
plt.title("f(x)=x^2 - 2")
plt.xlabel("x")
plt.ylabel("f(x)")
plt.legend()
# プロットの表示
plt.show()これらを実行すると、グラフを出力できます。
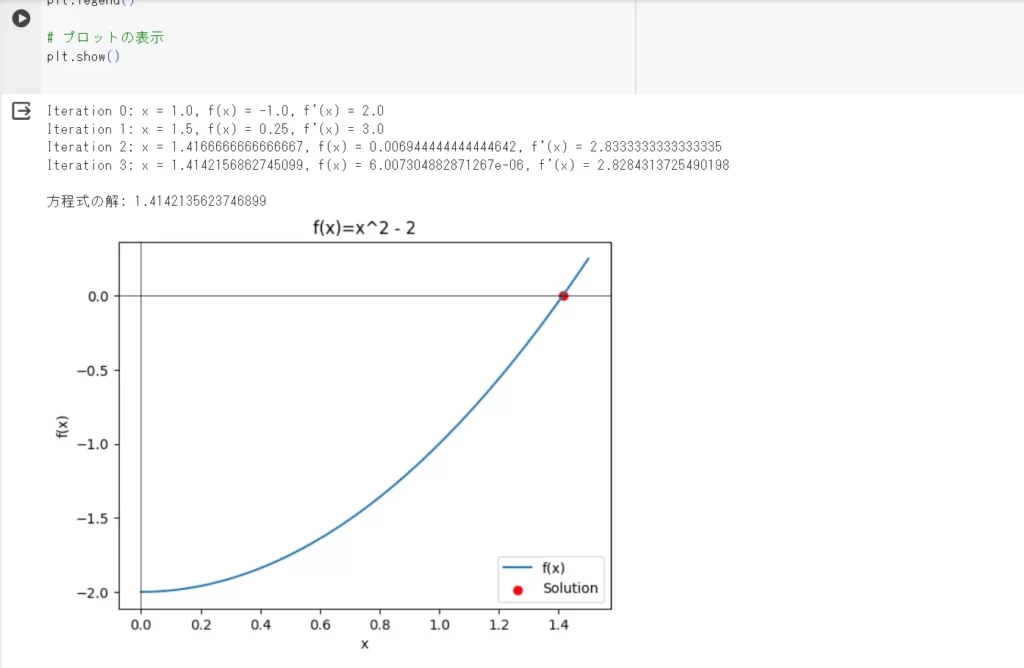
ライブラリを使用するニュートン法
scipy.optimize モジュールを使用すると、ニュートン法のような最適化アルゴリズムが簡単に利用できます。
from scipy.optimize import newton
def f(x):
return x**2 - 2
# 初期値
default = 1.0
# scipy.optimizeのnewton関数を使用
result = newton(f, default)
# 結果の表示
print(f"方程式の解: {result}")まとめ
ニュートン法は数学と計算機科学の分野で幅広く使用される優れた数値解法の一つです。その収束速度と適用範囲は数多くの問題で活かされていますが、注意が必要な点もあることを理解し、適切な状況で利用することが大切です。