Pythonで理解する統計学、第0回は、統計解析・データ分析(データサイエンス)などで使うライブラリの紹介です。
Pythonにはあらかじめ書かれた関数、メソッド、クラス、および変数などプログラムを簡単かつ効率的に書くことができるように設計されたライブラリが存在します。
本記事で紹介するライブラリはpipと呼ばれるパッケージマネージャを使用してインストールできます。
また、「Google Colaboratory」のようなクラウド上でPython開発環境を動作させるサービスは紹介するライブラリは搭載済みなので、インストールは不要です。
さらに、Tkinterと併用することで、アプリ化することも可能であり、ユーザーの数値入力によってグラフをプロットすることもできます。
- Numpy・Matplotlib・Pandas・Scipyライブラリの使い方を知りたい
- Google Colaboratoryについて知りたい
Numpy

NumPyは、”Numerical(数値)Python”の略で、科学的計算やデータ解析を行うための数値計算ライブラリで、大規模な数値計算や行列演算、信号処理、画像処理、機械学習などの科学技術計算を行うことができます。
NumPyは、科学技術計算でよく使用される数学関数、線形代数関数、フーリエ変換、ランダム数生成などの豊富な数学関数を提供しています。また、後述するライブラリやフレームワーク(pandas・ Matplotlibなど)と組み合わせて使用されることが多いです。
公式サイト:「Numpy」
Matplotlib

Matplotlibは、Pythonのデータ可視化ライブラリの1つであり、様々なグラフや図を作成することができます。グラフや図の種類は折れ線グラフ、散布図、棒グラフ、ヒストグラム、等高線図、3Dプロットと手広く扱うことができます。
公式サイト:「Matplotlib — Visualization with Python」
タイトルや凡例(軸の名前)などのグラフのカスタマイズは次のように書きます。
plt.title('タイトル')
plt.xlabel('定義域(X軸)の凡例')
plt.ylabel('値域(y軸)の凡例')また、グラフを出力するには次のように書きます。
MatplotlibはPNG形式の他にも、JPEG、PDF、SVGなど多くの形式に対応しています。
plt.savefig('ファイル名.png')その他、前述したNumPyとの統合も容易であり、
NumPyの配列を用いてグラフを作成することができます。
以下は、紹介したグラフや図の出力です。
折れ線グラフ
折れ線グラフは、データの連続的な変化を示すのに適しています。そのため、時間経過に伴うデータの変化を示すのによく使われます。また、複数のデータ系列を比較するのにも適しています。
折れ線グラフは、値の変化が滑らかであることが重要であるため、離散的なデータでは使用することができません。
離散的なデータ代表例は、テストの点数や「はい・いいえ」のような選択性アンケートなど整数値やカテゴリーなどです。
このようなデータを扱うときは、後述する棒グラフが優れています。
折れ線グラフのソースコードでは、sin関数の表現を紹介します。
import matplotlib.pyplot as plt
import numpy as np
# 折れ線グラフ
x = np.arange(0, 10, 0.1)
y = np.sin(x)
plt.plot(x, y)
plt.title('Sin Wave')
plt.xlabel('x')
plt.ylabel('y')
plt.savefig('line_graph_plot.png')
plt.show()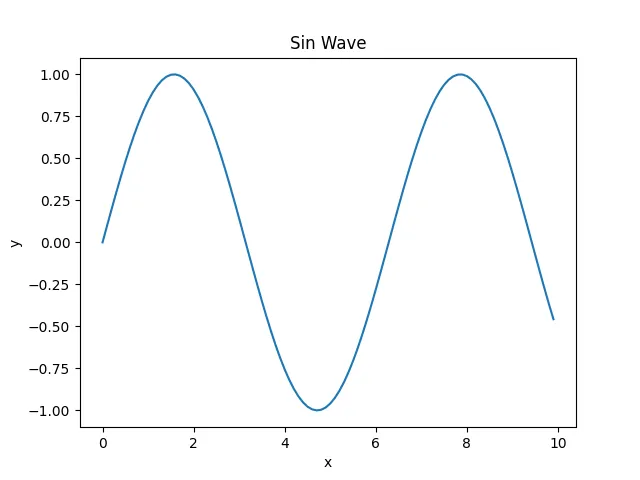
散布図
散布図は、2つの量的なデータの相関関係を視覚化するのに適しています。例えば、身長が高いと体重が重いのか(身長と体重の関係)、気温が高いとアイスクリームが売れるのか(気温とアイスクリームの販売数)の関係などが挙げられます。
散布図は、横軸と縦軸に2つの変数をとり、各変数の値を点としてプロットします。各点は、2つの変数の値を示し、データがどのように散らばっているかを確認することができます。
散布図を使用することで、相関関係があるかどうか、強さや方向性などを簡単に判断することができます。また、散布図に回帰直線を追加することで、2つの変数の関係をより詳しく調べることができます。
散布図は、統計解析や機械学習、ビジネス、科学などの多くの分野で広く使用されています。
import matplotlib.pyplot as plt
import numpy as np
# 散布図
x = np.random.normal(0, 1, 100)
y = np.random.normal(0, 1, 100)
plt.scatter(x, y)
plt.title('Scatter Plot')
plt.xlabel('x')
plt.ylabel('y')
plt.savefig('scatter_plot.png')
plt.show()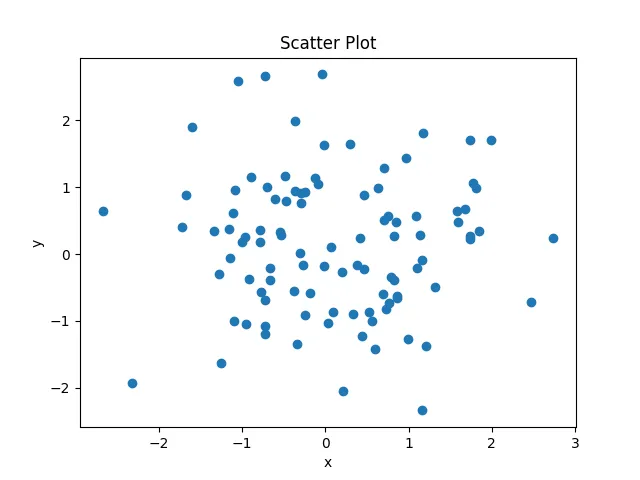
棒グラフ
棒グラフは、カテゴリーごとの値の比較や分布など離散的なデータを視覚的に表現するのに適しています。例えば、各都道府県の人口、各商品の売上、各月の降水量など、カテゴリーが限られているデータを表現するのに適しています。
棒グラフは、縦軸に数値を、横軸にカテゴリーをとり、それぞれのカテゴリーごとに棒を立てて表現します。棒の高さが数値を表し、カテゴリー間の棒の長さや厚さが比較の基準となります。
棒グラフを使用することで、カテゴリーごとの数値の大小関係や、分布の傾向などを簡単に判断することができます。また、複数の棒グラフを比較することで、データの変化や傾向を把握することができます。
棒グラフは、統計解析やビジネスのほか社会調査などの分野で広く使用されています。
import matplotlib.pyplot as plt
import numpy as np
# 棒グラフ
labels = ['Apple', 'Banana', 'Orange']
values = [20, 35, 25]
plt.bar(labels, values)
plt.title('Fruit Sales')
plt.xlabel('Fruit')
plt.ylabel('Sales')
plt.savefig('bar_graph_plot.png')
plt.show()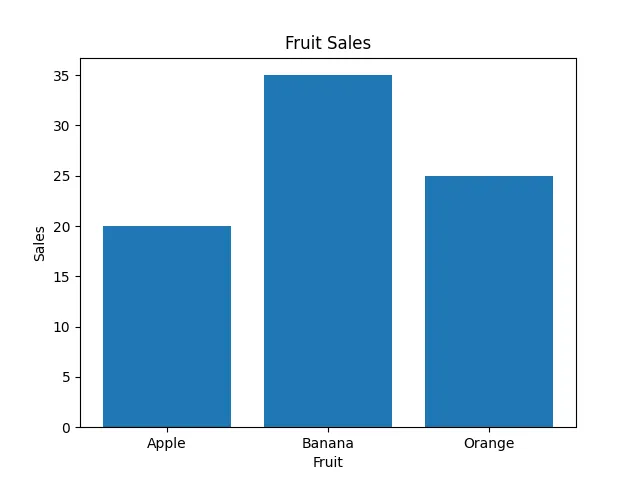
ヒストグラム
ヒストグラムは、数値データの分布を視覚化するために使用されます。例えば、身長や体重の分布、テストの点数の分布、経済的な指標の分布など、数値データの特徴を把握するのに適しています。
ヒストグラムは、横軸にデータの値の範囲を、縦軸にその範囲内にあるデータの個数や頻度をとり、各値の頻度を棒で表現します。各棒の高さが頻度を表し、横軸の範囲に対して棒の幅が設定されることがあります。
ヒストグラムを使用することで、データの分布の形状や平均値、分散などの統計的な特徴を簡単に把握することができます。また、複数のヒストグラムを比較することで、データの傾向や特徴を把握することができます。
ヒストグラムは、統計解析や機械学習、科学、ビジネスなどの分野で広く使用されています。
import matplotlib.pyplot as plt
import numpy as np
# ヒストグラム
data = np.random.normal(0, 1, 1000)
plt.hist(data, bins=30)
plt.title('Histogram')
plt.xlabel('Value')
plt.ylabel('Frequency')
plt.savefig('histogram.png')
plt.show()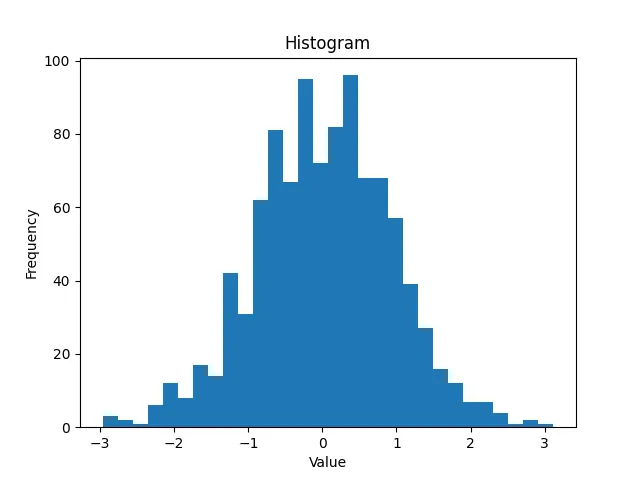
等高線図
等高線図は、2つの数値変数の関係を表現するグラフの一つで、3次元のデータを平面上に投影して、等高線状の線で表現します。例えば、高度と気温、海面水位と陸地の高さ、座標と気温など、2つの変数の関係を表現するのに適しています。
等高線図は、縦軸と横軸に2つの変数を、等高線で高さを表現します。各等高線は、同じ高さの地点を結んだ線で、高さが高いところほど密集していて、低いところほど疎になっています。また、等高線の間隔は、高低差に応じて調整され、等高線の密集度が高いところは急峻な地形、疎になっているところは平坦な地形を表します。
等高線図を使用することで、2つの変数の関係を視覚化し、それぞれの変数の影響を理解することができます。また、異なる高度や温度の地点の分布や傾向を把握することができます。
等高線図は、気象学や地理学、物理学、工学などの分野で広く使用されています。
import matplotlib.pyplot as plt
import numpy as np
# 等高線図
x = np.linspace(-5, 5, 100)
y = np.linspace(-5, 5, 100)
X, Y = np.meshgrid(x, y)
Z = np.sin(np.sqrt(X**2 + Y**2))
plt.contourf(X, Y, Z)
plt.colorbar()
plt.title('Contour Plot')
plt.xlabel('x')
plt.ylabel('y')
plt.savefig('contour_plot.png')
plt.show()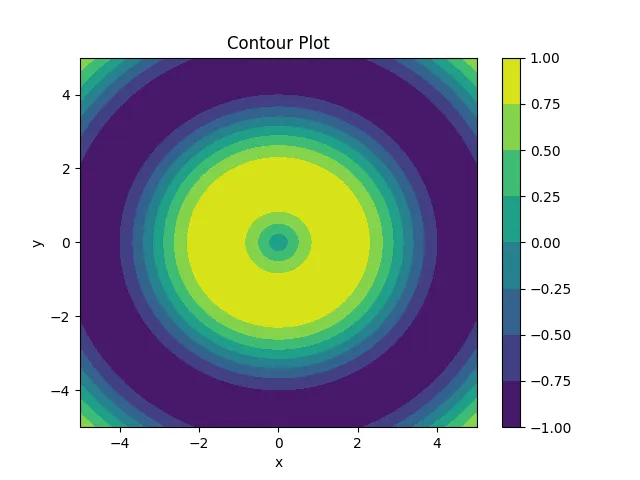
3Dプロット
3Dプロットは、3つの数値変数を使用して、立体的なグラフを作成するための手法です。例えば、2つの変数によって表される平面上での関係に加えて、3つ目の変数を追加して、立体的な関係を表現することができます。例えば、気温、風速、湿度など、3つの変数によって表される関係を表現するのに適しています。
3Dプロットは、3つの変数を縦軸、横軸、深度軸に割り当てて、3Dグラフを作成します。各点の座標は、3つの変数の値を表し、点の色やサイズなどを調整することで、さらに多様な情報を表現することができます。
3Dプロットを使用することで、3つの変数の関係を立体的に表現し、その変数同士の相関や傾向を把握することができます。また、多変量データの可視化に有効な手法であり、データの特徴や傾向を理解することができます。
3Dプロットは、科学や工学、ビジネスなど、多くの分野で使用されています。しかし、複雑なデータを扱う場合は、データの解釈が難しくなる場合があるため、注意が必要です。
import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
# 3Dプロット
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
x = np.linspace(-5, 5, 100)
y = np.linspace(-5, 5, 100)
X, Y = np.meshgrid(x, y)
Z = np.sin(np.sqrt(X**2 + Y**2))
ax.plot_surface(X, Y, Z)
ax.set_title('3D Surface Plot')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
plt.savefig('3d_surface_plot.png')
plt.show()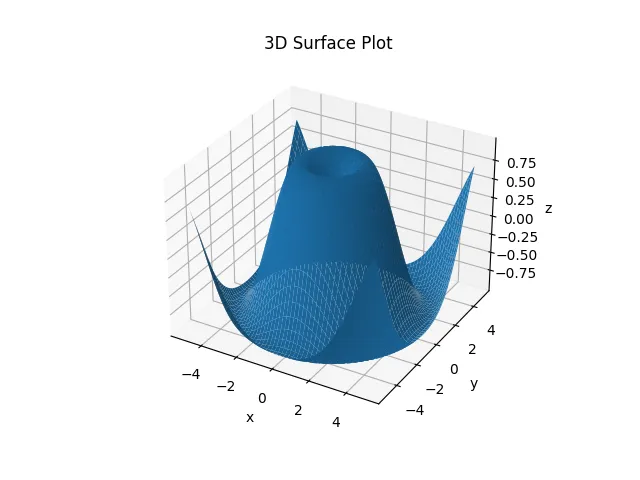
Pandas

Pandasは、Pythonで使われるオープンソースのデータ解析ライブラリです。Pandasは、NumPyの上に構築されており、より高水準のデータ操作機能を提供しています。主に、データフレームとシリーズの2つのデータ構造を提供しています。
データフレームは、2次元のラベル付きデータ構造で、列ごとに異なるデータ型を持つことができます。データフレームを用いることで、データの整形、加工、結合、集計、欠損値の処理など、様々なデータ処理を簡単に行うことができます。
データの読み込みや書き出しにも対応しており、CSV、Excel、SQL、JSON、HTML、XML、Parquetなどの様々な形式を扱うことができます。
シリーズは、1次元のラベル付きデータ構造で、NumPyの配列に似たデータ型を持ちます。シリーズは、データフレームの列または行として使用することができます。
Pandasは、データ処理に必要な機能を多数提供しており、データのクリーニング、変換、集計、可視化、機械学習など、様々なタスクを実行することができます。
Pandasは、金融、ビジネス、科学、技術、社会科学など、多くの分野で使用されています。
公式サイト:「pandas – Python Data Analysis Library」
Excelのテストの点数をPythonでグラフ化
Pandasを使って、Excelに入力された10点満点のテストの得点分布をヒストグラムに表示します。
以下の画像のようにAさんからZさん計26人のテスト点数を用意します。
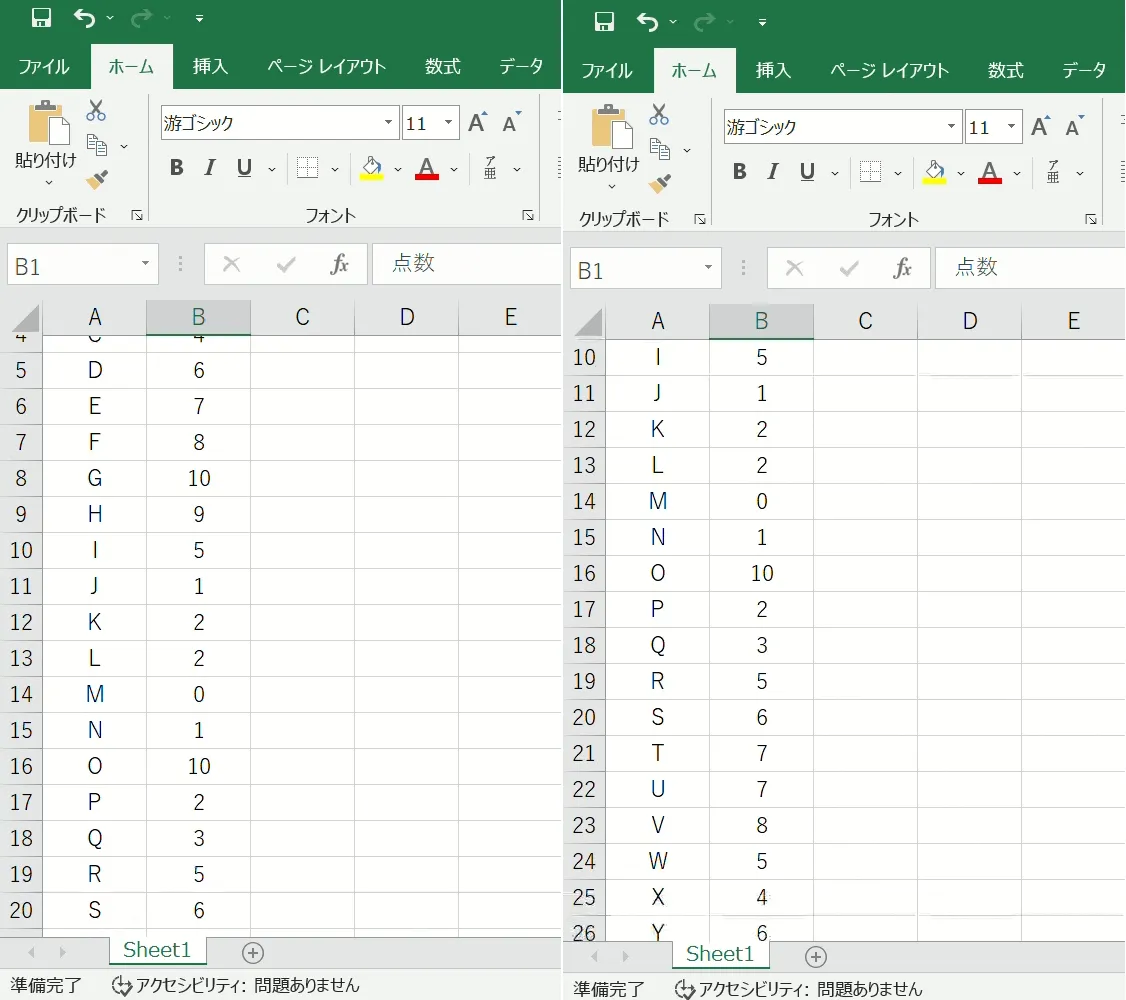
Excelのファイル(data.xlsx)はパスを指定するか、同じ場所に設置する必要があります。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# Excelファイルの読み込み
df = pd.read_excel('data.xlsx', sheet_name='Sheet1')
# 得点の配列を作成
scores = np.array(df['点数'])
# ヒストグラムの描画
plt.hist(scores, bins=10, range=(0, 10), alpha=0.5)
plt.xlabel('Points')
plt.ylabel('people')
plt.show()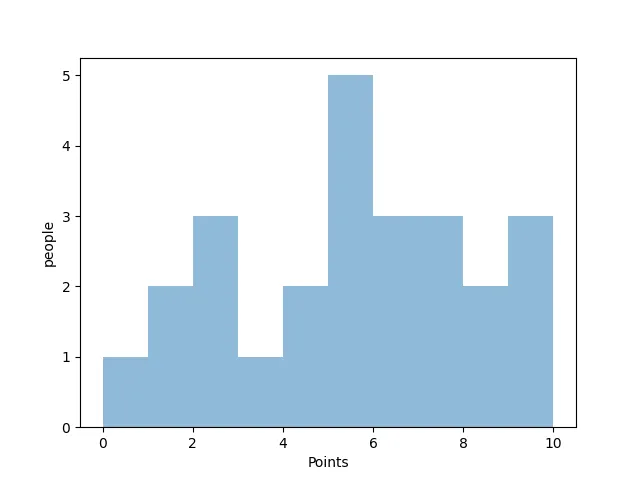
Scipy

Scipyは、科学技術計算において必要な数学的なアルゴリズムや関数を提供するPythonのライブラリです。NumPyをベースにしており、多くのサブパッケージを含んでいます。
- 線形代数
- 統計処理
- 最適化(Nelder-Mead法、BFGS法、Newton法、Levenberg-Marquardt法 etc.)
- 信号処理
- 画像処理
- 離散フーリエ変換
- 微分方程式の解法
- 積分の数値計算
- 特殊関数(ベータ関数、ガンマ関数、ベッセル関数、超幾何関数、楕円積分 etc.)の計算
このように、Scipyは、科学技術計算に必要な高度な数学的なアルゴリズムを使用できるため、機械学習・データ分析・信号処理・画像処理などの分野で広く使用されています。
公式サイト:「SciPy」
例えば、以下のようなScipyの機能があります。
- 最小二乗法による回帰分析
- フーリエ変換による信号の周波数解析
- 離散コサイン変換による画像圧縮
- 積分による確率分布関数の計算
以下に、Scipyを使った解析や計算を紹介します。
最小二乗法による回帰分析
最小二乗法による回帰分析は、2つの変数間の関係を調べる際によく使われます。例えば、身長と体重の関係を調べたり、気温とエアコンの使用量の関係を調べたりすることができます。
最小二乗法による回帰分析は、変数間の線形関係をモデル化して、そのモデルを用いて予測を行うことができます。また、回帰分析の結果から、変数間の関係の強さや方向性を評価することができます。
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit
# 最小二乗法による回帰分析
x = np.array([1, 2, 3, 4, 5])
y = np.array([2, 3, 5, 6, 8])
def func(x, a, b):
return a * x + b
popt, pcov = curve_fit(func, x, y)
plt.scatter(x, y)
plt.plot(x, func(x, *popt), 'r')
plt.show()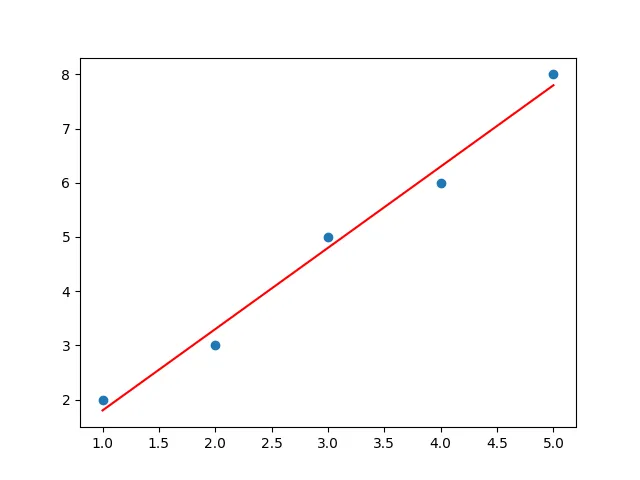
フーリエ変換による信号の周波数解析
フーリエ変換による信号の周波数解析は、信号処理や音声処理、画像処理などの分野でよく使われます。
信号処理(波形解析)において、フーリエ変換を用いて信号の周波数成分を解析することができます。
音声処理においては、音声ファイルを周波数成分に分解して、特定の周波数帯域の音声を取り出すことができます。
画像処理においては、フーリエ変換を用いて画像を周波数成分に分解して、特定の周波数帯域の画像情報を取り出したり、画像のフィルタリングを行ったりすることができます。
import numpy as np
import matplotlib.pyplot as plt
from scipy.fft import fft
# フーリエ変換による信号の周波数解析
N = 1000
T = 1.0 / 800.0
x = np.linspace(0.0, N * T, N)
y = np.sin(50.0 * 2.0 * np.pi * x) + 0.5 * np.sin(80.0 * 2.0 * np.pi * x)
yf = fft(y)
xf = np.linspace(0.0, 1.0 / (2.0 * T), N // 2)
plt.plot(xf, 2.0 / N * np.abs(yf[0:N // 2]))
plt.show()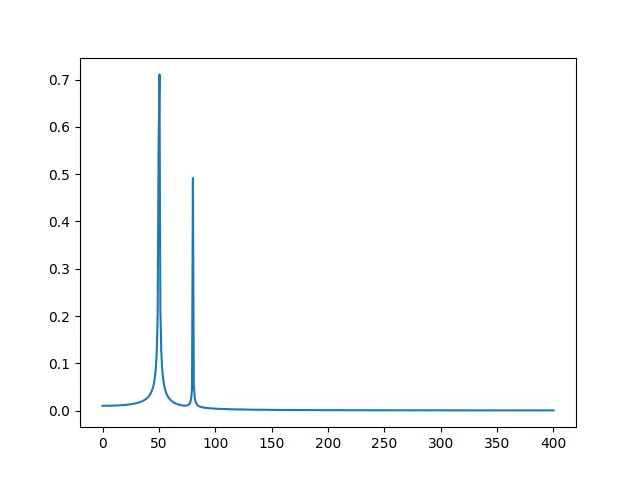
離散コサイン変換による画像圧縮
離散コサイン変換は、画像の圧縮やデータ圧縮に使用されます。
一般的に、画像の圧縮には、JPEGなどの標準的なフォーマットが使用されています。
JPEGフォーマットでは、離散コサイン変換が信号を周波数成分に分解して、高周波成分を除去することで、効率的に圧縮されます。また、データ圧縮の分野でも、離散コサイン変換がよく使用されます。
import numpy as np
import matplotlib.pyplot as plt
from scipy.fftpack import dct, idct
from scipy.misc import face
# 離散コサイン変換による画像圧縮
img = face(gray=True).astype('float')
img_dct = dct(dct(img.T, norm='ortho').T, norm='ortho')
coef = 0.1
mask = np.where(np.abs(img_dct) < coef, 0, 1)
img_dct *= mask
img_compressed = idct(idct(img_dct.T, norm='ortho').T, norm='ortho')
plt.imshow(img_compressed, cmap='gray')
plt.show()
積分による確率分布関数の計算
積分による確率分布関数の計算は、確率変数の値がある範囲に入る確率を求めたい場合に使用されます。
例えば、ある連続確率分布に従う確率変数Xが与えられた場合、その確率分布関数を積分することによって、Xがある範囲[a, b]に入る確率を求めることができます。
確率分布関数は、統計学や確率論などの分野でよく取り扱われます。
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import quad
# 積分による確率分布関数の計算
def integrand(x):
return np.exp(-x ** 2 / 2)
result= quad(integrand, -np.inf, np.inf)
x = np.linspace(-5, 5, 1000)
y = integrand(x)
plt.plot(x, y)
plt.title('Gaussian Distribution')
plt.xlabel('x')
plt.ylabel('Density')
plt.show()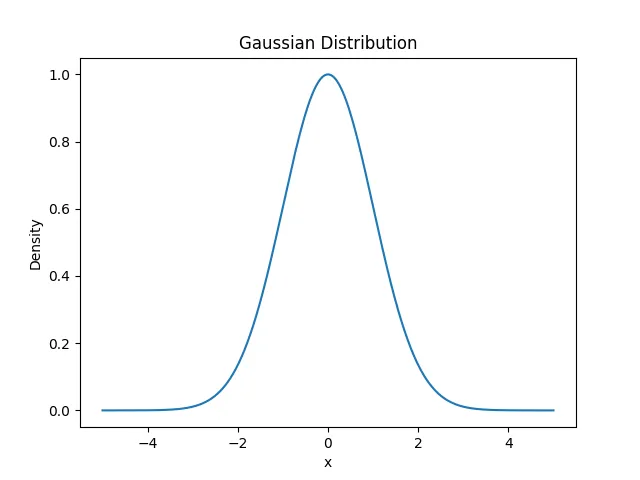
UdemyでPythonを学習
Udemyは、オンデマンド式の学習講座です。
趣味から実務まで使えるおすすめの講座を紹介します。
- 現役シリコンバレーエンジニアが教えるPython 3 入門 + 応用 +アメリカのシリコンバレー流コードスタイル
Pythonをインストールから環境設定、基本文法が学習
さらに暗号化、インフラ自動化、非同期処理についても学べます。
Pythonを基礎から応用まで学びたい人におすすめ
- みんなのAI講座 ゼロからPythonで学ぶ人工知能と機械学習 【2024年最新版】
機械学習ライブラリで文字認識や株価分析などを行う。
人口知能やニューラルネットワーク、機械学習を学びたい人におすすめ。
- 【世界で55万人が受講】データサイエンティストを目指すあなたへ〜データサイエンス25時間ブートキャンプ〜
統計分析、機械学習の実装、ディープラーニングの実装を学習。
データサイエンティストになりたい人におすすめ。
- 0から始めるTkinterの使い方完全マスター講座〜Python×GUIの基礎・応用〜
TkinterのGUIを作成から発展的な操作までアプリ実例を示して学習。
アプリ開発したい人におすすめ。
Jupyter・Google Colaboratory
Google Colaboratoryは、Googleが提供していて、Jupyter Notebookをベースとしたクラウド上で動作するPython開発環境です。GPUやTPUなどの高速な計算リソースも無料で利用できるため、データ解析や機械学習など、プログラミングやデータ分析に適しています。
公式サイト:「Jupyter」・「Google Colaboratory」
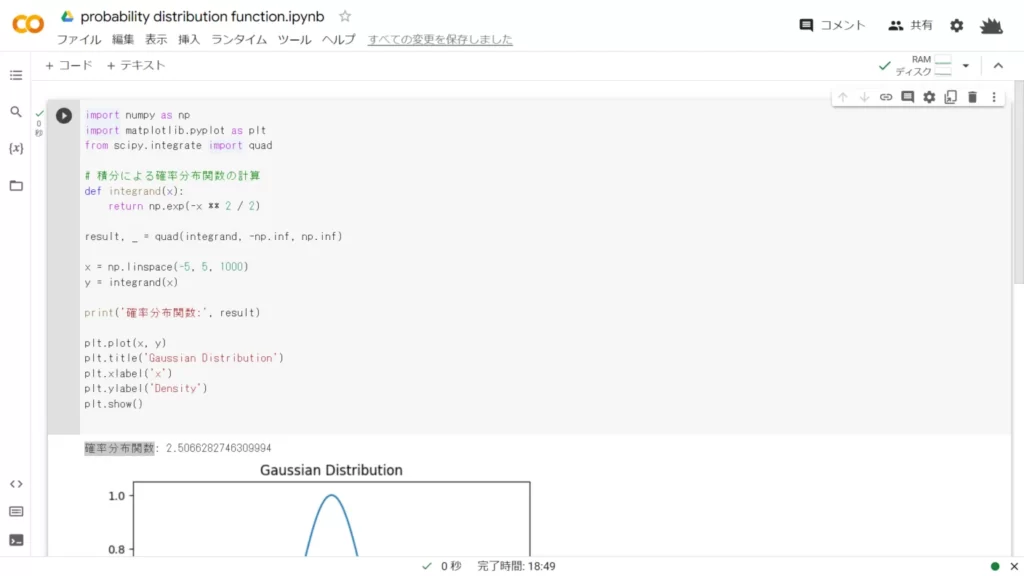
以下に、Google Colaboratoryを用いて、積分による確率分布関数の計算した様子を示します。
まとめ
今回は、統計解析・データ分析で使うライブラリを確認しました。
| ライブラリ | 用途 |
| Numpy | 数値計算 |
| Matplotlib | グラフや図を作成 |
| Pandas | データ解析(CSV、Excelなどの読み込みや書き出し) |
| Scipy | 数学的なアルゴリズムや関数を提供 |
これら4つは、統計学で非常によく使います。大量のデータもまとめることができるので、非常に便利です。